Как вычислить интеграл
Вычисление интеграла — операция, обратная дифференцированию. Позволяет выполнять операции по вычислению определенных и неопределенных интегралов. Множество всех первообразных функции f(x) (дифференциала f(x)dx) называется неопределенным интегралом от этой функции и обозначается ʃ f(x)dx.
Для вычисления интеграла необходимо ввести подынтегральное выражение (подынтегральную функцию) с переменной х.
Пример расчёта интеграла
Имея следующую задачу по определению интеграла приступим к работе.
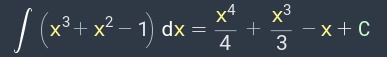
Теория вычисления интегралов
Вычисление интеграла – это одна из основных задач математического анализа, которая позволяет находить площади под кривыми, объемы тел вращения, работу силы и многие другие величины. Интегралы бывают неопределенные и определенные, и методы их вычисления различаются.
Неопределенный интеграл
Неопределенный интеграл функции `f(x)` представляет собой семейство всех первообразных этой функции и обозначается как `∫f(x)dx`. Для его вычисления используются различные методы:
- Прямое интегрирование: Если функция является табличной, то есть её первообразная известна и находится в таблице интегралов, то достаточно просто взять эту первообразную. Например, `∫x^n dx = (x^(n+1))/(n+1) + C`, где `C` – константа интегрирования.
- Метод подстановки (замены переменной): Если функция имеет сложный вид, можно попробовать упростить её, сделав замену переменной. Например, если `u = g(x)`, то `dx = du/g'(x)`, и интеграл принимает вид `∫f(g(x))g'(x)dx = ∫f(u)du`.
- Интегрирование по частям: Этот метод основан на формуле интегрирования произведения функций `∫u dv = uv — ∫v du`. Он полезен, когда подынтегральное выражение является произведением двух функций, одна из которых легко интегрируется, а другая – дифференцируется.
- Разложение на простые дроби: Если функция представляет собой рациональную дробь, то есть отношение двух многочленов, то её можно разложить на простейшие дроби, каждую из которых интегрировать отдельно.
Определенный интеграл
Определенный интеграл функции `f(x)` на интервале `[a, b]` обозначается как `∫_a^b f(x)dx` и представляет собой число, которое геометрически соответствует площади фигуры, ограниченной графиком функции, осью `x` и вертикальными прямыми `x = a` и `x = b`. Для его вычисления можно использовать следующие методы:
- Теорема о среднем значении для интегралов: Если функция `f(x)` непрерывна на `[a, b]`, то существует такое число `c` из этого интервала, что `∫_a^b f(x)dx = f(c)(b — a)`.
- Методы численного интегрирования: Когда функция слишком сложна для аналитического интегрирования, используют численные методы, такие как метод прямоугольников, трапеций или Симпсона.
- Использование первообразной: Если известна первообразная `F(x)` функции `f(x)`, то определенный интеграл можно вычислить по формуле Ньютона-Лейбница: `∫_a^b f(x)dx = F(b) — F(a)`.
Вычисление интегралов – это навык, который требует практики и понимания основных свойств интегрирования. Существуют также компьютерные программы и онлайн-калькуляторы, например, вверху на этой странице, которые могут помочь в нахождении интегралов, особенно для сложных функций.